Trabajando con arreglos y matrices
Por omisi�n, las dimensiones de la pantalla han sido ajustadas para una sola celda. Mucha gente utiliza la calculadora sin enterarse de que puede trabajar con matrices o de modo mas general con arreglos de n�meros. Y en muchos campos de los problemas probablemente no se requiere de estas funciones. . Pero si necesita trabajar con matrices o vectores aritm�ticos, resolver conjuntos de ecuaciones simultaneas, trabajar con n�meros complejos, hacer conversiones entre sistemas de co-ordenadas, lo mas seguro es que necesite de estas potentes funciones. Tenga en cuenta que si est� utilizando una computadora de manos con una versi�n de WindowsCE superior a la 3.0 (generalmente los dispositivos viejos) las funciones de matriz no estar�n disponibles.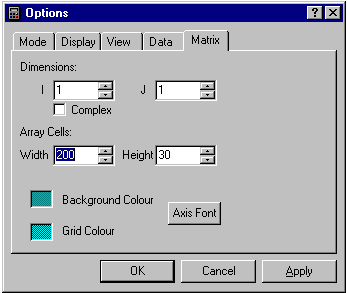
Las dimensiones de la cuadricula de pantalla pueden ser ajustadas utilizando la pesta�a Matrix del cuadro de dialogo de Opciones. Cuando las dimensiones han de superar 1x1, est�n disponibles funciones adicionales como se describe mas abajo cuando el bot�n Shift es pulsado. Algunas funciones son dependientes de ciertas restricciones en las dimensiones para que puedan estas disponibles. Si la dimensi�n I es puesta exactamente en Dos (2), entonces puede activar la casilla de verificaci�n ?Complex? para poder hacer uso de los n�meros complejos.
Puede ser necesario agrandar la pantalla cambiando el tama�o de la ventana de la calculadora para poder visualizar la cuadricula de valores. En WindowsCE (por ej: Pocket PC), no estar� en disposici�n de agrandar la calculadora en su totalidad, pero puede hacer el �rea de visualizaci�n de pantalla mas grande reduciendo el tama�o de los botones, y posiblemente descartando las cinco filas de botones de funciones. Puede tambi�n tener la necesidad de experimentar con los tama�os de las letras para los botones y la pantalla. Tambi�n puede reducir la precisi�n para hacer posible visualizaciones de valores en columnas mas angostas. Una vez que haya seleccionado el modo de arreglo o matriz, la pantalla hacer recordar de alguna manera las hojas de calculo tales como Excel.
Presentando arreglos y Matrices.
Cuando use arreglos de n�meros (Vea la secci�n Mode ), la pantalla es dividida en un arreglo de celdas en una cuadricula. El color de esta cuadricula es ajustado por las tres opciones de color y fuente en la parte inferior de la P�g. De dialogo Matrix.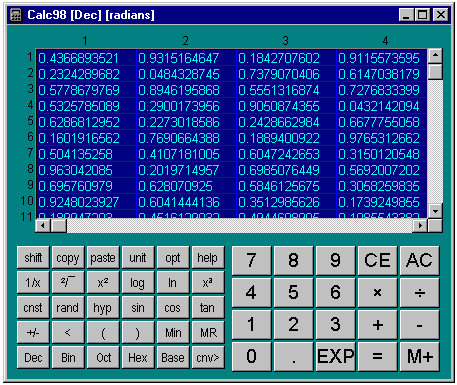
Las dimensiones de cada celda (en pixeles) son definidas en las casillas num�ricas Width y Height bajo el titulo ?Array Cells?
Los ejes son dibujados utilizando la fuente especificada utilizando el cuadro de dialogo de fuentes al pulsar el bot�n Axis Font. El color de fondo es ajustado utilizando el seleccionador de en medio de los tres disponibles. (Averiguar pues esto no coincide muy bien en la practica real).
Aritm�tica Simple con arreglos
Cuando se inicia el modo de arreglos se podr� ver que todas las celdas del arreglo son seleccionadas y si se hace un calculo simple, este se repetir� en cada celda. Esta es la manera como trabaja la aritm�tica simple de los arreglos. Aplicando cada operaci�n a todas las celdas, y claramente esto no es particularmente �til. Pero en el modo de arreglo un numero de botones tienen funciones nuevas o especializadas (realzadas). Por ejemplo, oprimiendo el bot�n rand se produce un arreglo de n�meros aleatorios (aseg�rese de estar en el modo decimal).
En los ejemplos a continuaci�n, asumimos que se est� empleando l�gica de precedencia algebraica. Si est� utilizando RPN se necesita introducir los valores en la pila y utilizar las entradas de los operadores posteriores en su modo normal.
- Index
Si se hace click en el bot�n Rand el bot�n se convierte en Ind que asigna a cada celda su propio n�mero �ndice. Ahora podemos hacer algo medianamente �til: Seleccione modo decimal, modo de grados y haga un arreglo de 10 x 9. Haga click en Ind (Shift + rand). Haga click en + luego en 1 (note que todas las celdas son rellenadas de 1?s). Haga clic en ?=? todas las celdas tienen ahora el valor de su propio �ndice +1, por ejemplo valores desde 1 hasta 90. Ahora haga clic en el bot�n Sin y tendr� una tabla instant�nea de los senos de todos los �ngulos en grados. Si el resultado parece incierto, revise si se acord� de poner el modo de Angulo en (grados) degrees.
Ahora supongamos que desea repetir esta operaci�n con otras funciones trigonom�tricas, ra�z cuadrada, etc. , pero no quiere repetir el procedimiento de sumar 1 a cada �ndice de celda cada vez. Simplemente guarde el resultado intermedio en la memoria utilizando para ello el bot�n Min. Todas las memorias trabajan en modo de arreglo, (aunque solo el valor del primer elemento del arreglo es mostrado en la ventana de dialogo cuando se selecciona memoria).
Seleccionado celdas y rangos de celdas
Inicialmente, todas las celdas son seleccionadas, pero se puede seleccionar una sola celda haciendo click en ella con el mouse o con el l�piz indicador en el WindowsCE. Cuando se selecciona una celda, las restantes son atenuadas. Se siente natural utilizar el l�piz de este modo. Se puede seleccionar tambi�n un grupo de celdas rectangular oprimiendo el bot�n izquierdo del mouse en una celda y liber�ndolo despu�s de haberlo movido a otra celda (procedimiento general de arrastre) . (En computadores de l�piz se oprime el l�piz sobre una celda y se mueve por la superficie de la pantalla para levantarlo despu�s en alguna otra celda). Alternativamente se puede seleccionar una celda y luego emplear la combinaci�n SHIFT + Selecci�n en otra celda para indicar un rango de celdas. Se puede desplazar la pantalla antes del segundo paso de este procedimiento, haciendo posible seleccionar un rango de celdas as� no sea posible ver la totalidad de ellas en la pantalla al mismo tiempo.
Finalmente se puede utilizar el teclado del computador (o teclado virtual) con las teclas de control del cursor (teclas de flecha) para hacer una selecci�n de �rea. Esto trabaja en todos los modos excepto en el de tiempo, cuando las teclas de flecha controlan el cronometro. Las teclas Home y End (Inicio y Fin) seleccionan la primera y ultima celda respectivamente. Si un rango de celdas es seleccionado, el rango de celdas (pero no los valores contenidos) se mover� alrededor de la cuadricula como si estuviera utilizando las teclas del cursor. El bot�n next en el teclado principal puede tambi�n ser utilizado para mover una sola celda por vez, las teclas alfanum�ricas del computador INSERT O (INS) hacen la misma cosa. Este procedimiento es extremadamente �til cuando se han de introducir valores en cada celda paso a paso una por una.
Se pueden seleccionar todas las celdas haciendo click en al parte exterior de la cuadricula si el �rea de presentaci�n es mayor que la cuadricula o utilizando alguna de las t�cnicas arriba nombradas. Si la cuadricula es mas grande que el �rea de pantalla, han de aparecer, barras de desplazamiento para mover la cuadricula y el �rea exterior de la cuadricula no Ser� visible, pero existe un peque�o bot�n donde se juntan las dos barras que puede ser utilizado para seleccionar todas las celdas. Existe tambi�n una opci�n ?Select All? en el Menu Edit. Haciendo Click en "AC" se seleccionan todas las celdas para borrarlas todas de su contenido.
Una vez que se haya seleccionado una celda o un rango de ellas, todas las operaciones aritm�ticas subsiguientes actuaran en esas celdas �nicamente. Seleccionar una sola celda le permite hacer c�lculos completos en esa celda solamente. Se puede entonces mover a otra celda o incluirla en un grupo de celdas mas extenso y hacer mas operaciones o c�lculos. Ejemplo: Se desea una tabla de n�meros y sus ra�ces cuadradas hasta 10. Primero ajuste las dimensiones del arreglo en 2x11. Seleccione todas las celdas en la primera columna y haga clic en ind (SHIFT ?rand?). Seleccione la segunda columna e indexe de la misma manera que la primera columna. Con la segunda columna seleccionada aun haga clic en el bot�n Sqrt.
Usando copiado y pegado
El bot�n de copy (o Ctrl-C en el teclado) puede se usado para copiar el contenido de las celdas seleccionadas en el portapapeles. Puede entonces seleccionar una sola celda y utilizar el bot�n Paste (o Ctrl-V en el teclado) para pegar los datos que hab�an sido copiados, comenzando en la celda seleccionada. Si las dimensiones del grupo de celdas es demasiado grande para el tama�o del arreglo especificado, los datos restantes que no caben ser�n descartados. Si hace selecci�n de un grupo de celdas y luego utiliza paste, solo las celdas seleccionadas ser�n actualizadas desde el portapapeles, as� el portapapeles contenga un numero mayor de datos a ser pegados. Si el portapapeles contiene un peque�o grupo de celdas que la selecci�n de celdas hecha solo se llenaran el numero de celdas procedentes del portapapeles y el resto de la selecci�n permanecer� inalterado.
Copiar datos al portapapeles tambi�n pone los datos a disposici�n de otra aplicaci�n tal como un procesador de palabra o una hoja de calculo. El mismo proceso puede ser utilizado en reversa para importar datos desde otras aplicaciones. Ejemplo: Utilizando el ejemplo de arriba, aseg�rese que todas las celdas est�n seleccionadas y haga clic en el bot�n de copiar. Corra un programa tal como Excel (o Pocket Excel en un dispositivo de mano), seleccione una celda y seleccione Pegar (paste) del men� de edici�n del programa. Los datos son ahora puestos a disposici�n de la aplicaci�n y se pueden hacer operaciones o c�lculos, o se pueden imprimir o anexarlos a otra hoja de calculo.
Como se dijo se puede hacer la operaci�n contraria, se pueden copiar en el portapapeles datos de otra aplicaci�n y pegarlos en el arreglo de la calculadora. O mas aun se pueden utilizar las funciones de copiado y pegado como un medio conveniente de mover bloques de datos dentro de un arreglo, o guardar datos para posteriores procesos de c�lculo. Debido a que el portapapeles le permite un solo bloque de datos por vez, pueda que requiera del uso de las memorias para procesos de calculo mas complejos. Tambi�n debe tener en mente que los datos guardados en el portapapeles como texto en cualquier formato de presentaci�n como el modo actualmente seleccionado. Esto significa que si esta utilizando un peque�o numero de lugares decimales habr� una perdida de precisi�n comparado con el uso de la memoria en la calculadora, por as� decirlo. tambi�n significa que si se guardan datos en el portapapeles provenientes del modo Hexadecimal y luego se hace el cambio para el modo decimal, el portapapeles todav�a contendr� datos en modo Hexadecimal que ser�n interpretados como decimal. Esto probablemente no dar� el resultado deseado.
Aritm�tica de Matrices
La aritm�tica de matrices tiene reglas especiales. La adici�n y substracci�n de matrices est�n definidas convenientemente como la suma o la diferencia de los elementos individuales lo que viene a ser igual que las operaciones aritm�ticas simples descritas anteriormente que no requieren por consiguiente de ning�n trabajo extra de nuestra parte.
Ejemplo: sumar las matrices
Ajuste el tama�o del arreglo en 2x2. Seleccione la primera celda utilizando el mouse /l�piz o la tecla de HOME en su teclado alfanum�rico. Oprima el bot�n [1] seguido del bot�n [next] (o la tecla INS ). Esto ingresara el valor de 1 en la primera celda y movera el puntero o cursor hacia la pr�xima celda disponible. Introduzca el [2] seguida de [next] que autom�ticamente le llevar� a la pr�xima celda. Ingrese el [3] y el [4] de la misma manera como los dos anteriores pasos, el [next] final selecciona todas las celdas (recuerde que si una celda simple es seleccionada para una operaci�n aritm�tica, actuar� para esa unica celda). Ahora haga clic en el bot�n [+] (si est� utilizando RPN se utilizar� [Enter] y [+] en el proximo paso). Se introduce la segunda matriz del mismo modo que la primera, es decir valor, next, valor, next y asi sucesivamente hasta el final [next] que selecciona todas las celdas para la operaci�n aritm�tica. Entonces haga clic en el el bot�n [=] para ver el resultado:
Multiplicar una matriz por un escalar
Una matriz puede se multiplicada por un escalar de una manera bien simple introduciendo primero la matriz y luego asegur�ndose que todos los elementos estan seleccionados, entonces se hace clic en el bot�n
seguido por un valor (que aparecer� en todas las celdas) y luego [=] para obtener el producto.
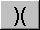- Producto de Matrices
Las reglas para la multiplicaci�n de matrices son mas complicadas. Si solamente se utiliza el bot�n de multiplicaci�n de la misma manera que el bot�n de sumar como se describi� anteriormente lo que haremos ser� una multiplicaci�n de una matriz por un escalar de las celdas individuales. Algunas veces esto es lo que deseamos, pero para la multiplicaci�n de matrices necesitamos el operador apropiado el cual es obtenido pulsando el bot�n [Shift] , entonces el bot�n [*] cambia a )( como el operador multiplicativo para las matrices.
Ejemplo: Hallar el producto de las dos matrices cuadradas:
Dos matrices pueden ser multiplicadas si el n�mero de columnas de la primera es igual al n�mero de filas de la segunda matriz. Si este es el caso se dice que las matrices est�n conformadas. Cuando se ingresan matrices que no son cuadradas nos hemos de asegurar simplemente que la cuadricula tiene por lo menos tantas filas y columnas como la matriz mas grande. Entonces dejamos todos los elementos sin usar como cero. La aritm�tica trata de la conformaci�n, debido a que cualquier conjunto de filas y columnas no conformadas ser�n multiplicadas por cero.
Ejemplo de multiplicar matrices no cuadradas:
(
) (
)
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 1 | 2 | 5 | 1 | 0 |
| 2 | 3 | 4 | 1 | 3 | 1 |
| 3 | 2 | 0 | 1 | 6 | 2 |
| 4 | 0 | 0 | 0 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0 | 0 |
, ingrese entonces la segunda matriz..
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 0 | 4 | 0 | 0 | 0 |
| 2 | 6 | 2 | 0 | 0 | 0 |
| 3 | 1 | 4 | 0 | 0 | 0 |
| 4 | 3 | 8 | 0 | 0 | 0 |
| 5 | 1 | 7 | 0 | 0 | 0 |
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 20 | 36 | 0 | 0 | 0 |
| 2 | 35 | 55 | 0 | 0 | 0 |
| 3 | 21 | 74 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0 | 0 |
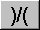- Division de Matrices
Por integridad se ha incluido la funci�n de divisi�n de matrices, la cual es la equivalente a la PRE-multiplicaci�n del numerador de la matriz por el inverso del denominador.
Ejemplo: Evaluar la siguiente expresi�n de matriz
Revisar:
Se ha de tener en cuenta que la multiplicaci�n de matrices no es conmutativa , de tal modo que el orden en que se efectua la multiplicaci�n es importante.
Resolviendo un conjunto de ecuaciones lineales. La divisi�n de matrices nos brinda un f�cil, recordado e intuitivo metodo de resolver los conjuntos de ecuaciones lineales dividiendo simplemente la matriz que contiene las constantes por el coeficiente de la matriz.
Ejemplo:
Dado el conjunto de ecuaciones lineales:
10x + 2y - 10z =
16 )
-10x + 5y + 12z = 7
)
4x + 6y + 10z
= 36 )
Esto puede ser pasado como una expresi�n de matrices:
( 10 2 -10 )
( x ) ( 16 )
( -10 5 12 ) x
( y ) = ( 7 )
( 4 6 10
) ( z )
( 36 )
Para resolver las ecuaciones para (x,y,z) hacemos el equivalente de dividir ambos lados por el coeficiente de la matriz, de modo que:
( x ) ( 16 )
( 10 2 -10
)
( y ) = ( 7 )
/ ( -10 5
12 )
( z ) ( 36
) ( 4
6 10 )
(en realidad estaremos pre-multiplicando por el inverso)
Primero ajuste las dimensiones de la matriz en 3 x 3 e introduzca las constantes como una matriz de 3 x 1 columnas (solo deje los otros elementos como 0).
| 1 | 2 | 3 |
| 16 | 0. | 0. |
| 7 | 0. | 0. |
| 36 | 0. | 0. |
Asegur�ndose que todas las celdas est�n seleccionadas hacemos clic en Shift y luego en el bot�n divide (que se presenta con la etiqueta ")/(").
En el siguiente paso introducimos el coeficiente de la matriz como una matriz de 3 x 3.
| 1 | 2 | 3 |
| 10 | 2 | -10 |
| -10 | 5 | 12 |
| 4 | 6 | 10 |
Finalmente se oprime el bot�n [=] para obtener el resultado de los valores para x, y,z como otra matriz de 3 x 1:
| 1 | 2 | 3 |
| 3 | 0. | 0. |
| 2 | 0. | 0. |
| 1 | 0. | 0. |
Que presenta como soluci�n x = 3, y = 2, z = 1.
En la practica, es probablemente buena idea, introducir el coeficiente de la matriz primero y guardarla en la memoria lista para su uso, debido a que se consume tiempo. Tambi�n se puede utilizar una de las otras memorias para constantes. Esto le permite retroceder y corregir errores sin tener que introducir todos los valores de nuevo. Sea cuidadoso cuando ingrese n�meros negativos en utilizar el bot�n de cambio de signo [+/-] y no utilizar el bot�n de sustracci�n, que evaluar�a los datos ingresados hasta el momento.
Se pueden producir resultados err�neos cuando el conjunto de ecuaciones sea muy complicado o enredado o no tenga �nica soluci�n, y errores de redondeo puedan conducir a resultados imprecisos, si es que se produce un resultado. En estos casos se necesita utilizar t�cnicas num�ricas mas sofisticadas que aquellas que estamos brindando como funciones incorporadas.
- Transposici�n
El bot�n T calcula la transposici�n de una matriz, si la matriz no es cuadrada, la mayor matriz contenida es transpuesta, mientras que los elementos por fuera del cuadrado son dejados intactos.
- Invertir
Utilice este bot�n (que se obtiene al oprimir shift y el bot�n 1/X) para invertir una matriz. Dependiendo de los valores de los elementos, puede ser posible que no se obtenga el inverso de la matriz, en cuyo caso se debe obtener un error de sobrecarga (overflow) . Un ejemplo es el inverso de una matriz Cero (o nula) , que es el equivalente de tomar el reciproco de 0 en la aritm�tica escalar.
La matriz inversa puede ser usada como un medio de resolver un conjunto de ecuaciones lineales, aunque existen mejores metodos numericos. Ver el ejemplo de divisi�n de matrices arriba estudiado.
- Determinante
Esto calcula el determinante de una matriz, y es hallado utilizando el bot�n shift con el bot�n "<" (retroceso). El resultado es presentado en la forma de una matriz escalar, p.e. cada uno de los elementos diagonales contiene la derterminante calculada.
- Matriz Unitaria
El bot�n unit genera una matriz unitaria p.e. una matriz con elementos cero excepto para los elementos diagonales rellenados con 1 (unos). Se obtiene con la combinaci�n de los botones Shift (y el bot�n Unit que se ha convertido en I)
Se puede usar la matriz unitaria para generar otras matrices diagonales. Por ejemplo multiplicar la matriz unitaria por una constante, o hacer una simple multiplicaci�n escalar con la matriz unitaria para obtener los elementos diagonales de una matriz dada.
Trabajando con vectores
Si en la pag. Opciones/Matriz el valor de I es 2 o 3, estan disponibles funciones adicionales para vectores.
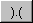- Producto Escalar
Este bot�n calcula el (punto) producto escalar de dos vectores. El resultado es un vector escalar que es representado como su product con la matriz unitaria.
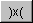- Vector Producto
Este bot�n calcula el vector (cruz) producto de dos vectores.
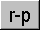- Rectangular a Polar
Convierte coordenadas de sistema rectangular (o cartesiano) a coordenadas polares. Use
y el bot�n
Ejemplo: Ajuste el valor de celdas para I a 2, celdas para J en 1. Modo de angulo en degrees. Introduzca el valor de 1.0 en ambas celdas para obtener las coordenadas (x, y) :
| 1. | 1. |
Ahora:
, resultado:
| 1.4142135624 | 45. |
El resultado se encuentra coordenadas (r, theta) donde 1.4142... es la raiz cuadrada de 2 y el angulo theta (?), es 45 grados.
Si el n�mero I de celdas es ajustado a 3 las coordenadas rectangulares son dadas como (x, y, z) y el resultado es expresado en coordenadas cil�ndricas polares (r, theta (?), z).
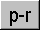- Polar a Rectangular
Convierte coordenadas (cartesianas) de polar a rectangular. Use el bot�n
y el bot�n 
button.
. Tenga cuidado de introducir el �ngulo theta (?) en las unidades correctas dependiendo de modo actual de �ngulos usado.
Problemas de ejemplo
Flujo de tr�fico
Una proposici�n para un sistema de una sola via se considera el problema de una matriz cuadrada. El trafico existente fluye como se muestra en la gr�fica y ha sido medido. Asumiendo que no existe un cambio en el trafico externo, se propone hallar el flujo de veh�culos por hora por la calle Acacia (A) , las carrera Bond (B), el paseo Cornish (C), y la Avenida Durham (D) , dados los valores de flujo de trafico medidos en las v�as adyacentes.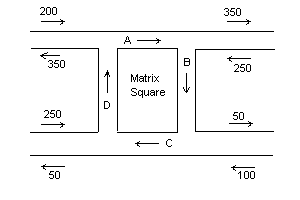
Un primer vistazo nos muestra un problema insoluble. Para que hallar soluci�n, se ha de hallar las condiciones de los l�mites de las v�as. Podemos apreciar que el tr�fico entrante se ha de balancear con el tr�fico saliente anotando que 800 veh�culos por hora entran en Matrix Square y 800 por hora lo abandonan. Bien.
Ahora necesitamos juntar la informaci�n que tenemos disponible. Comenzando con la confluencia entrando en la calle Acacia, El flujo de tr�fico neto por hora consiste en 200 entrando en el empalme y 350 saliendo m�s cualquiera que venga desde la Avenida Durham menos el trafico de la calle Acacia entonces:
200 - 350 + D - A = 0, or -A + D = 150
Tomando los otros empalmes de la misma manera:
A - B = 100
B - C = -50
C - D = -200
En forma de matriz:
( -1 0 0 1 )
( A ) ( 150
)
( 1 -1 0 0 )
( B ) ( 100
)
( 0 1 -1 0 )
x ( C ) = ( -50
)
( 0 0 1 -1 )
( D ) ( -200 )
Para obtener la soluci�n para A, B, C y D necesitamos introducir las constantes como una matriz de columnas de 4x1 y
| 1 | 2 | 3 | 4 |
| 150. | 0. | 0. | 0. |
| 100. | 0. | 0. | 0. |
| -50. | 0. | 0. | 0. |
| -200. | 0. | 0. | 0. |
Entonces utilice el boton de dividir matrices (")/(" = shift + "/") y luego introduzca el coeficiente de la matriz.
| 1 | 2 | 3 | 4 |
| -1. | 0. | 0. | 1. |
| 1. | -1. | 0. | 0. |
| 0. | 1. | -1. | 0. |
| 0. | 0. | 1. | -1. |
El resultado, una matriz de 4x1, nos da A = 50, B = -50, C = 0 and D = 200.
| 1 | 2 | 3 | 4 |
| 50. | 0. | 0. | 0. |
| -50. | 0. | 0. | 0. |
| 0. | 0. | 0. | 0. |
| 200. | 0. | 0. | 0. |
Dotados de esta informaci�n, el ingeniero de tr�fico sabe que la avenida Durham necesita manejar sustancialmente mas trafico que la calle Acacia, y que el paseo Cornish puede dejarse para peatones, y puede alertar a la polic�a que 50 carros , estar�n yendo en contrav�a por la Carrera Bond en cualquier hora t�pica. El ingeniero puede tambi�n desear revisar las condiciones limites que no est�n especificadas completamente, debido a que una cantidad arbitraria de trafico circulante puede ser a�adido mientras todav�a se satisfacen lasa restricciones.
Se puede notar que una gran cantidad de elementos de esta matriz son cero. Esto es caso com�n cuando se representan problemas f�sicos de redes o cuadriculas de puntos o vol�menes de control, que resultan en matrices muy dispersas con bandas de elementos no cero. Otro ejemplo es dado mas abajo.