N�meros Complejos
Se pueden realizar calculos de aritmetica compleaja ajustando en la pag. Options/Matriz el valor de las direcciones de celdas I en exactamente 2, y activando la casilla de verificaci�n de N�meros complejos.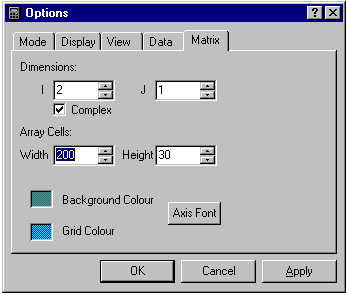
Si el numero de celdas para I es ajustado a otro valor, no le ser� permitido abandonar el cuadro de dialogo con la casilla de verificaci�n activada para complejos. Si se ajusta el valor de J para m�s de una celda puede entonces trabajar con un arreglo de una dimensi�n de n�meros complejos.
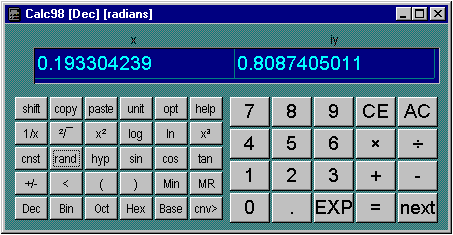
Con la activacion de los numeros complejos los encabezados de las columnas son �x� e �iy� para indicar las partes reales e imaginarias de cada numero. En un PC de escritorio es posible que le gustara reajustar la disposici�n del teclado para modo apaisado, para trabajar con la aritm�tica de los complejos, debido al espacio extra que se necesita en pantalla . Se pueden tambien ajustar las dimensiones de pantalla de tal modo que no se necesiten las barras de desplazamiento.
Sed pueden efectuar operaciones aritmeticas simples para los nunmeros complejos, o experimentar con exponenciacion y funciones logaritmicas o funciones trascendentales. Para ingresar valores seleccione la parte real o la imaginaria como lo haria con elementos de un arreglo como se describi� en la Secci�n de Arreglos y Matrices. . Si selecciona la parte real o imaginaria de un numero complejo, la logica aritmetica trabajar� sobre el numero como un todo, no solo sobre la parte seleccionada.
Puede realizar operaciones "normales" con n�meros reales, ajustando la parte imaginaria a cero. Por supuesto que en ciertos casos esto dara lugar a numeros complejos. El famoso ejemplo:
Ingrese un 1, cambie su signo ("+/-"). Resultado:
| x | iy |
| -1. | 0. |
Ahora obtenga la ra�z cuadrada. Resultado:
| 0. | 1. |
Las funciones aritmeticas actuan de la misma manera que para los numeros reales. La adicion de complejos es simplemente la adicion de arreglos, pero la multiplicaci�n y divisi�n son ligeramente complicadas. Por ejemplo:
(x1 + i.y1)(x2 + i.y2) = x1x2 + i.x1y2 + i.x2y1 + i 2.y1y2 = (x1x2 -y1y2) + i.(x1y2 + x2y1)
Otros ejemplos se dan mas abajo:
Matematica compleja Basica
Las funciones aritmeticas actuan de la misma manera que para los numeros reales. La adicion de complejos es simplemente la adicion de arreglos, pero la multiplicaci�n y divisi�n son ligeramente complicadas. Por ejemplo:(x1 + i.y1)(x2 + i.y2) = x1x2 + i.x1y2 + i.x2y1 + i 2.y1y2
= (x1x2 -y1y2) + i.(x1y2 + x2y1)
Plano Complejo.
Para convertir numeros desde componentes reales e imaginarios a modulo y argumento en el plano complejo (diagrama de Argand), utilice los botones normales [r-p] y [p-r]. Esto son obtenidos utilizando el bot�n [Shift] cuando reemplazan las etiquetas de los botones [+] y [-] aritm�ticos. Una vez convertidos la calculadora "no sabe" si los valores estan en coordenadas polares, y Ud. debe convertirlos de regreso a la forma cartesiana para continuar con los calculos. El argumento estar� expresado en grados, radianes o gradientes dependiendo del modo de angulo seleccionado.Ejemplo:
Visualizar los numeros complejos en el plano complejo es un medio potente de pensar acerca de los componentes reales e imaginarios de los n�meros. El comportamiento de las operaciones aritm�ticas puede ser comprendido mas f�cilmente considerando los equivalentes geom�tricos en el plano complejo. Por ejemplo, para obtener la raiz cuadrada de un n�mero complejo, tome la raiz cuadrada del modulo y divida el argumento por dos. Se puede verificar esto utilizando la calculadora para obtener la raiz cuadrada de varios numeros y convirti�ndolos a coordenadas polares.