property>solid angle
What is Solid Angle?
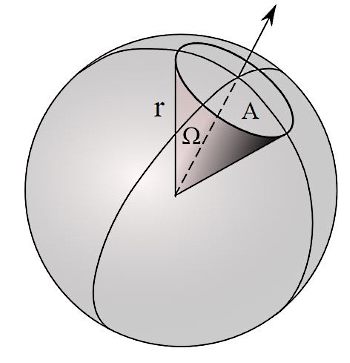
The solid angle is the angle created in three-dimensional space that an object subtends at a point. Solid angle is a measure of how big an object appears to an observer when looking from that point. The symbol for solid angle is Ω (Greek letter omega).
A solid angle can be defined in terms of an area on the surface of a sphere which is centred at the vertex of the angle. This is the equivalent of defining a planar angle in terms of the length of arc on a circle subtended to the centre. Solid angle can also be defined as an angle formed by three or more planes intersecting at a common point (the vertex). The SI unit of solid angle is the steradian (sr). The solid angle of a complete sphere is 4π sr. The solid angle corresponding to the face of a cube measured at the centre is 2π/3 sr. One steradian is equal to (180/π)2 square degrees.
The concept of a solid angle and the term steradian can be perplexing to people only acquainted with ordinary angles. Everybody knows what a 90° angle looks like and even referring to it as π/2 radians is relatively easy to understand. But it is a different matter altogether with solid angles since it must be imagined in three-dimensional space without an obvious reference.
First let us consider a reference circle and an ordinary angle. The angle θ can also be explained in terms of the arc. Let s be the length of the arc and r be the radius of the circle. The ordinary angle in radians is given by θ = (s/r). or, in degrees it is defined as θ = (360/2π)(s/r). Now assume a cone which intersects the sphere of radius R. Consider S be the area of surface subtended by the intersection of the sphere and the cone. The solid angle is defined Ω = (S/r²). This defines the solid angle in steradians.
If the surface covers the entire sphere then the number of steradians is 4π. If you know the solid angle Ω in steradians then you can easily calculate the corresponding area of the surface of any sphere from the expression S = R2Ω, where R is the radius of the sphere.
The practical applications of solid angles include the definition of luminance and luminous intensity and the derivation of Gauss's law. It is also used in mathematical modelling in Boundary Element Methods to calculate potentials. Solid angles are necessary to identify the size of ligands in metal complexes, and to calculate the strength of the magnetic and electric field for a given charge distribution.
The Sun and Moon are about the same apparent size when seen from the earth. They occupy an area of 0.001% of the celestial hemisphere, which equates to a solid angle of approximately 6 × 10-5 steradians.